Setting up automatic SSCHA simulations on clusters

Manual submission

The SSCHA calculation comprises three main steps iterated until convergence:

1. The generation of a random ensemble of ionic configurations

2. Calculations of energies and forces on the ensemble

3. The SSCHA free energy minimization

In the first hands-on session, you configured the code to do these iterations automatically. Thanks to the ASE EMT force field, the code can automatically compute energies, forces, and stress tensors without user interaction.

However, if you need to compute energies and forces from an ab initio calculation like DFT, you may want to run the DFT code on a different machine, like a cluster.

You can use the manual submission if you want more control over the procedure.

We will compute the sulfur hydride (superconductor with \(T_c = 203\) K), using a DFT code like quantum Espresso to calculate energy and forces.

The harmonic phonons (computed using quantum Espresso) is provided in the directory 02_manual_submission, where you can find the input and output files of the quantum espresso calculation to calculate the harmonic phonons, and the dynamical matrices, named dyn_h3s_harmonic_1, dyn_h3s_harmonic_2 and dyn_h3s_harmonic_3.

They respect the naming convention so that each file contains a different q point: since we are using a 2x2x2 mesh to sample the Brillouin zone of phonons, the different q points are ordered in three separate files, each one grouping the star of q (the q points related by symmetry operations).

We start by plotting the dispersion of the harmonic dynamical matrix. Please write in a file the following script and run it.

import cellconstructor as CC, cellconstructor.Phonons
import cellconstructor.ForceTensor
import ase, ase.dft

import matplotlib.pyplot as plt
import numpy as np

dyn = CC.Phonons.Phonons("dyn_h3s_harmonic_", 3) # Load 3 files

PATH = "GHNPGN"
N_POINTS = 1000

# Use ASE to get the q points from the path
band_path = ase.dft.kpoints.bandpath(PATH,
    dyn.structure.unit_cell,
    N_POINTS)

# Get the q points in cartesian coordinates
q_path = band_path.cartesian_kpts()

# Get the values of x axis and labels for plotting the band path
x_axis, xticks, xlabels = band_path.get_linear_kpoint_axis()

# Perform the interpolation of the dynamical matrix along the q_path
frequencies = CC.ForceTensor.get_phonons_in_qpath(dyn, q_path)

# Plot the dispersion
fig = plt.figure()
ax = plt.gca()
ax.set_title("Harmonic H3S Phonon dispersion")
for i in range(frequencies.shape[-1]):
   ax.plot(x_axis, frequencies[:, i], color = 'r')


for x in xticks:
   ax.axvline(x, 0, 1, color='k', lw=0.4) # Plot vertical lines for each high-symmetry point

# Set the labels of the axis as the Brilluin zone letters
ax.set_xticks(xticks)
ax.set_xticklabels(xlabels)

ax.set_ylabel("Frequency [cm-1]")
ax.set_xlabel("q-path")
plt.tight_layout()
plt.savefig("harmonic_h3s_dispersion.png")
plt.show()

You should see the figure Dispersion of the harmonic phonons of H3S.

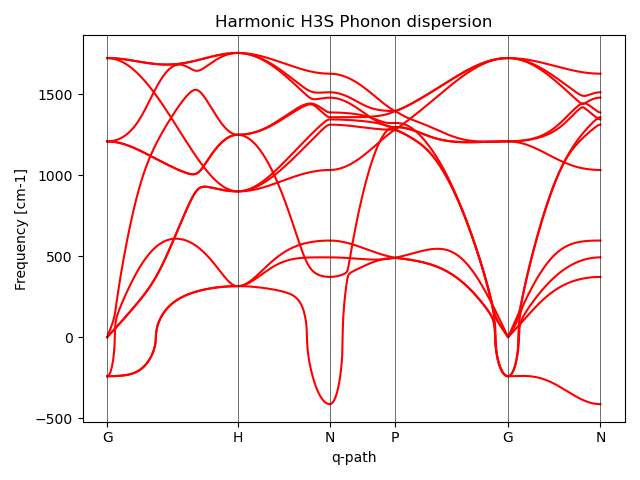
The dispersion presents imaginary phonons throughout most of the Brillouin zone. To start the SSCHA, we need a positive definite dynamical matrix. Since the starting point for the SSCHA does not matter, we may flip the phonons to be positive:

where \(m_a\) is the mass of the a-th atom, \(\omega_\mu\) is the frequency of the dynamical matrix, and \(e_\mu\) is the corresponding eigenvector. This operation can be performed with the command

dyn.ForcePositiveDefinite()

and save the results into start_sscha1, start_sscha2, and start_sscha3 with

dyn.save_qe("start_sscha")

import cellconstructor as CC, cellconstructor.Phonons
import sscha, sscha.Ensemble
import numpy as np

# Fix the seed so that we all generate the same ensemble
np.random.seed(0)

# Load the dynamical matrix
dyn = CC.Phonons.Phonons("start_sscha", nqirr=3)

#[ apply here the needed changes to dyn ]

# Prepare the ensemble
temperature = 300 # 300 K
ensemble = sscha.Ensemble.Ensemble(dyn, temperature)

# Generate the ensemble
number_of_configurations = 10
ensemble.generate(number_of_configurations)

# Save the ensemble into a directory
save_directory = "data"
population_id = 1
ensemble.save(save_directory, population_id)

dyn.Symmetrize()

import ase, ase.visualize
import cellconstructor as CC, cellconstructor.Structure

struct = CC.Structure.Structure()
struct.read_scf("data/scf_population1_1.dat")
ase_struct = struct.get_ase_atoms()
ase.visualize.view(ase_struct)

#!/bin/bash

HEADER_FILE=espresso_header.pwi
DATA_DIR=data
POPULATION=1

# Define a directory in which to save all the input files
TARGET_DIRECTORY=$DATA_DIR/input_files_population$POPULATION

mkdir -p $TARGET_DIRECTORY

for file in `ls $DATA_DIR/scf_population${POPULATION}*.dat`
do
    # Extract the configuration index
    # (the grep command returns only the expression
    #  that matches the regular expression from the file name)
    index=`echo $file | grep -oP '(?<=population1_).*(?=\.dat)'`

    target_input_file=$TARGET_DIRECTORY/structure_${index}.pwi

    # Copy the template header file
    cp $HEADER_FILE $target_input_file

    # Attach after the header the structure
    cat $file >> $target_input_file
done

mpirun -np NPROC pw.x -i input_file.pwi > output_file.pwo

#!/bin/bash

N_CONFIGS=10
POPULATION=1
PATH_TO_DIR="data/output_espresso"
N_ATOMS=32


ENERGY_FILE="data/energies_supercell_population${POPULATION}.dat"

# Clear the energy file
rm -rf $ENERGY_FILE

for i in `seq 1 10`
do
    filename=${PATH_TO_DIR}/structure_$i.pwo
    force_file=data/forces_population${POPULATION}_$i.dat
    stress_file=data/pressures_population${POPULATION}_$i.dat

    # Get the total energy
    grep ! $filename | awk '{print $5}' >> $ENERGY_FILE
    grep force $filename | grep atom | awk '{print $7, $8, $9}' > $force_file
    grep "total   stress" $filename -A3 | tail -n +2 | awk '{print $1, $2, $3}' > $stress_file
done

import sscha, sscha.Ensemble, sscha.SchaMinimizer
import sscha.Utilities
import cellconstructor as CC, cellconstructor.Phonons

POPULATION = 1

dyn = CC.Phonons.Phonons("start_sscha", 3)
ensemble = sscha.Ensemble.Ensemble(dyn, 0)
ensemble.load("data", population = POPULATION, N = 10)

minim = sscha.SchaMinimizer.SSCHA_Minimizer(ensemble)
minim.init()

# Save the minimization details
ioinfo = sscha.Utilities.IOInfo()
ioinfo.SetupSaving("minim_{}".format(POPULATION))


minim.run(custom_function_post = ioinfo.CFP_SaveAll)
minim.finalize()
minim.dyn.save_qe("final_sscha_dyn_population{}_".format(POPULATION))

sscha-plot-data.py minim_1

Automatic submission with a cluster

In the previous section, you made all the steps to run a sscha calculation manually. This consists of iterating through the following steps:

1. generating the input files for Espresso,

2. transferring them to a cluster,

3. submitting the calculations,

4. retrieving the outputs,

5. reload the ensemble

6. run the free energy minimization

In this section, we learn how to automatize these passages. We must set up the interaction between the SSCHA library and the HPC cluster running the DFT calculations. As of June 2023, this automatic interaction is only supported for quantum Espresso and SLURM-based clusters. However, writing plugins to support different DFT codes and cluster schedulers should be easy.

The configuration of the DFT parameter has been introduced in the previous hands-on session; thus, we skip and provide a file called espresso_calculator.py, which defines a function get_h3s_calculator returning the calculator object for quantum Espresso with the input parameters for H3S.

We focus instead on the configuration of the cluster. Create a new file called cluster.py. The following script provides an example to connect to a cluster with username sschauser and login node my.beautiful.cluster.eu:

import cellconstructor as CC, cellconstructor.Phonons
import sscha
import sscha.Cluster

import sys, os


def configure_cluster(cluster_workdir = "H3S"):
    cluster = sscha.Cluster.Cluster(hostname = "sschauser@my.beautiful.cluster.eu")

    cluster.use_memory = True
    cluster.ram = 180000
    cluster.use_partition = True
    cluster.partition_name = "workstations"
    cluster.account_name = "my_allocation_resources"
    cluster.n_nodes = 1
    cluster.use_cpu = False
    cluster.custom_params["get-user-env"] = None
    cluster.custom_params["cpus-per-task"] = 2
    cluster.custom_params["ntasks-per-node"] = 48
    cluster.time = "12:00:00"
    cluster.n_cpu = 48
    cluster.n_pool = 48
    cluster.job_number = 12
    cluster.batch_size = 2

    home_workdir=os.path.join("$HOME", cluster_workdir)
    scratch_workdir = os.path.join("/scratch/$USER/", cluster_workdir)
    cluster.workdir = home_workdir
    cluster.add_set_minus_x = True  # Avoid the set -x
    cluster.load_modules = f"""

module purge
module load intel
module load intel-mpi
module load intel-mkl
module load quantum-espresso/6.8.0-mpi

export OMP_NUM_THREADS=$SLURM_CPUS_PER_TASK

mkdir -p {scratch_workdir}
cp $HOME/espresso/pseudo/* {scratch_workdir}/
"""

    def cp_files(lbls):
        extrain = f"cd {scratch_workdir}\n"
        extraout = "sleep 1\n"
        for lbl in lbls:
            extrain += f"cp {home_workdir}/{lbl}.pwi {scratch_workdir}/\n"
            extraout += f"mv {scratch_workdir}/{lbl}.pwo {home_workdir}/\n"

        return extrain, extraout

    # Add the possibility to copy the input files
    cluster.additional_script_parameters = cp_files

    # Force to open a shell when executing ssh commands
    # (Otherwise the cluster will not load the module environment)
    cluster.use_active_shell = True
    cluster.setup_workdir()

    # Check the communication
    if not cluster.CheckCommunication():
        raise ValueError("Impossible to connect to the cluster.")

    return cluster

This file contains all the information to connect with the cluster that you can customize to adapt to your HPC center.

Let us dive a bit into the options.

The first thing to know how to configure is the ssh host connection. For example, if I connect to a cluster using the command

ssh sschauser@my.beautiful.cluster.eu

You have to specify the entire string sschauser@my.beautiful.cluster.eu inside the hostname key at the first definition of the cluster. If you have an ssh config file enabled, you can substitute the hostname with the name in the configuration file corresponding to a HostName inside .ssh/config located in your home directory.

The best procedure is to enable a public-private key without encryption. You can activate the encryption if you have a wallet system in your PC that keeps the password saved, but in this case, the user must log in with the screen unlocked to work.

If the HPC does not allow you to configure a pair of ssh keys for the connection and requires the standard username/password connection, you can add the pwd keyword in the definition of the cluster. This is not encouraged, as you will store your password in clear text inside the script (so if you are in a shared workstation, remember to limit the read access to your scripts to other users, and do not send the script accidentally to other people with your password).

For example:

cluster = sscha.Cluster.Cluster(hostname="sschauser@my.beautiful.cluster.eu", pwd="mybeautifulpassword")

The other options are all standard SLURM configurations, as the amount of ram, name of partition, and account for the submission, number of nodes, total time, and custom parameters specific for each cluster These parameters are transformed into the submission script for slurm as

#SLURM --time=12:00:00
#SLURM --get-user-env
#SLURM --cpus-per-task=2
# [...]

Most variables have the use_xxx attribute; if set to False, the corresponding option is not printed. In the last version of SSCHA, if you manually edit a variable, it should automatically set the corresponding use_xxx to true.

cluster.use_partition = True
cluster.partition_name = "workstations"
cluster.account_name = "my_allocation_resources"

Most clusters must run on specific partitions; in this case, activate the partition flag with the use_partition variable and specify the appropriate partition_name. Also, most of the time, the computational resources are related to specific accounts indicated with account_name.

Particular attention needs to be taken to the following parameters

cluster.n_nodes = 1
cluster.time = "12:00:00"
cluster.n_cpu = 48
cluster.n_pool = 48
cluster.job_number = 12
cluster.batch_size = 2

These parameters are specific for the kind of calculation.

1. n_nodes specifies the number of nodes

2. time specifies the total time

3. n_cpu specify how many processors to call quantum Espresso with

4. n_pool is the number of pools for the quantum espresso parallelization; it should be the greatest common divisor between the number of CPUs and K points.

5. batch_size how many pw.x calculations to group in the same job (executed one after the other without queue time).

6. job_number how many jobs will be submitted simultaneously (executed in parallel, but with queue time).

The total time requested must be roughly the time expected for a single calculation multiplied by the batch_size. It is convenient to overshoot the requested time, as some configurations may take a bit more time.

The workdir is the directory in which all the input files are copied inside the cluster. This cluster uses a local scratch for the submission (the job must copy all the input on a local scratch of the node and then copy back the results to the shared filesystem). If no local scratch is requried, then we can set the working directory (usually a shared scratch) with the command

cluster.workdir = "/scratch/myuser/"

However, this submission script (as ekhi) must work on a shared workdir, which is inside the home directory. Therefore, we must tell the cluster to copy the files from the workdir to the local scratch before and after each calculation. This is done by setting a custom function, executed for each calculation

def cp_files(lbls):
    extrain = f"cd {scratch_workdir}\n"
    extraout = "sleep 1\n"
    for lbl in lbls:
        extrain += f"cp {home_workdir}/{lbl}.pwi {scratch_workdir}/\n"
        extraout += f"mv {scratch_workdir}/{lbl}.pwo {home_workdir}/\n"

    return extrain, extraout

# Add the possibility to copy the input files
cluster.additional_script_parameters = cp_files

Each cluster must load modules to run a calculation. All the modules and other commands to run before the calculations are stored in the text variable load_modules

cluster.load_modules = f"""
module purge
module load intel
module load intel-mpi
module load intel-mkl
module load quantum-espresso/6.8.0-mpi

export OMP_NUM_THREADS=$SLURM_CPUS_PER_TASK

mkdir -p {scratch_workdir}
cp $HOME/espresso/pseudo/* {scratch_workdir}/
"""

The specific of the modules to load depends on the cluster, in this case, we also create the local scratch directory and copy the pseudopotential.

To check the connection and set up the working directory (create it on the cluster if it does not exist) use the

cluster.setup_workdir()

if not cluster.CheckCommunication():
    raise ValueError("Cluster connection failed!")

import cellconstructor as CC, cellconstructor.Phonons
import sscha, sscha.Ensemble

# Import the two python scripts for the cluster and espresso configurations
import espresso_calculator
import cluster

# Generate an ensemble with 10 configurations
dyn = CC.Phonons.Phonons("start_sscha", 3)
ensemble = sscha.Ensemble.Ensemble(dyn, 300)
ensemble.generate(10)

# Get the espresso and cluster configurations
espresso_config = espresso_calculator.get_calculator()
cluster_config = cluster.configure_cluster()

# Compute the ensemble
ensemble.compute_ensemble(espresso_config, cluster=cluster_config)

# Save the ensemble (using population 2 to avoid overwriting the other one)
ensemble.save("data", 2)

import cellconstructor as CC, cellconstructor.Phonons
import sscha, sscha.Ensemble
import sscha.SchaMinimizer, sscha.Relax

# Import the two python scripts for the cluster and espresso configurations
import espresso_calculator
import cluster

# Generate an ensemble with 10 configurations
dyn = CC.Phonons.Phonons("start_sscha", 3)
ensemble = sscha.Ensemble.Ensemble(dyn, 300)

# Get the espresso and cluster configurations
espresso_config = espresso_calculator.get_calculator()
cluster_config = cluster.configure_cluster()

# Setup the minimizer
minimizer = sscha.SchaMinimizer.SSCHA_Minimizer(ensemble)

# Setup the automatic relaxation
relax = sscha.Relax.SSCHA(minimizer, espresso_config,
        N_configs=10,
        max_pop=3,
        save_ensemble=True,
        cluster=cluster_config)

# Setup the IO to save the minimization data and the frequencies
ioinfo = sscha.Utilities.IOInfo()
ioinfo.SetupSaving("minimization_data")

# Activate the data saving in the minimization
relax.setup_custom_functions(custom_function_post=ioinfo.CFP_SaveAll)

# Perform the NVT simulation
relax.relax(get_stress=True)

# Save the data
relax.minim.finalize()
relax.minim.dyn.save_qe("final_dyn")