This tutorial was prepared for the 2023 SSCHA School by Raffaello Bianco. You can see here the video os the hands-on session:
The material needed for this tutorial can be downloaded here.
Theoretical introduction
The SCHA phonons are non-interacting quasiparticles that already include anharmonic effects (i.e. interaction between standard harmonic phonons) at some level. However, anharmoncity causes interaction between the SCHA phonons too. The interactions between phonons causes a change of their energy spectrum: from the overlap of simple Dirac-delta functions centered around the SSCHA phonon frequencies, to the overlap of Lorentzians with finite width (i.e. the quasiparticles have finite lifetime) and centered around shifted energies, or structures even more complex (when the anharmoncity is so strong that the quasiparticle picture has to be abandoned). For each \(\boldsymbol{q}\) of the Brillouin zone, the SCHA phonons energy spectrum \(\sigma(\boldsymbol{q},\Omega)\) is given by Eq.(70)
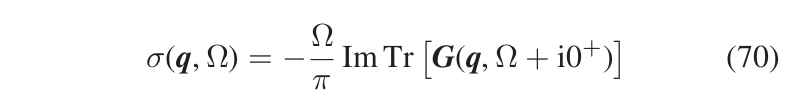
where \(\boldsymbol{G}\) is the SCHA phonons Green function, given by \(\boldsymbol{G}=\boldsymbol{G}^{(0)}+\boldsymbol{G}^{(0)}\boldsymbol{\Pi}\,\,\boldsymbol{G}\), with \(\boldsymbol{G}^{(0)}\) the Green function of the noninteracting SCHA phonons, and \(\boldsymbol{\Pi}\) their selfenergy taking into account the interaction (in order to make easier the comparison with the literature, here and in the subsequent equations, the equation numbers refer to the paper here https://arxiv.org/abs/2103.03973). The SSCHA code allows to compute these quantities, even if in the current implementation the selfenergy can be computed only in the bubble approximation (Eq. (75))
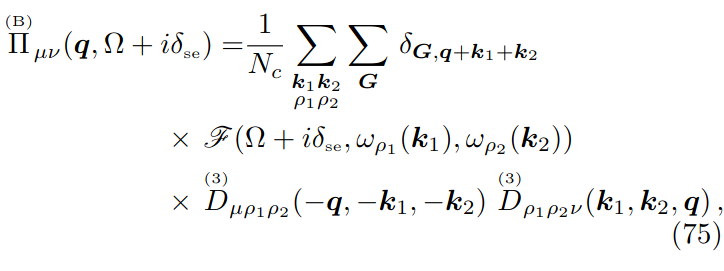
i.e. the self-energy terms including the 4th order FCs are discarded. In this equation \(\delta_{\scriptscriptstyle{\text{se}}}\) is an infinitely small positive number (a smearing parameter), that in actual calculations has to be chosen, toegher with the integration \(\boldsymbol{k}\)-grid, in order to find converged results.
The code, in addition to providing the ability to compute the spectral function through the full formula Eq. (70), allows for various approximations to be used in order to both compute the spectral function with reduced computational cost and conduct an analysis of the different contributions to the spectral function provided by each mode. The main approximation is to negeclet the off-diagonal terms in the self-energy written in the SCHA-modes basis set. In other words, we can negelct the possibility that the interaction mixes different SCHA phonons. In that case, the total spectrum is given by the the sum of the spectrum of each mode, \(\sigma_{\mu}(\boldsymbol{q},\Omega)\), as shown in Eq.(78),
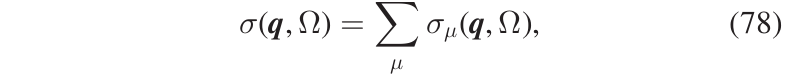
with \(\sigma_{\mu}(\boldsymbol{q},\Omega)\) having a generalized Lorentzian-like expression shown in Eq.(79)
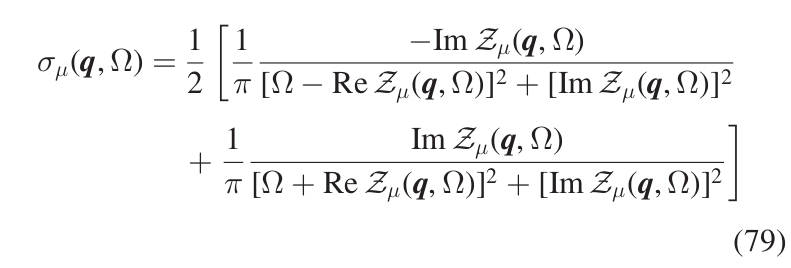
with \(\mathcal{Z}_{\mu}(\boldsymbol{q},\Omega)\) defined in Eq.(80)
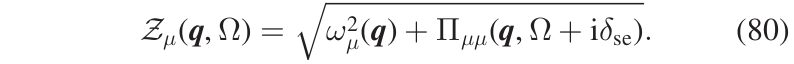
where \(\omega_{\mu}(\boldsymbol{q})\) is the frequency (energy) of the SCHA phonon \((\boldsymbol{q},\mu)\), and \(\boldsymbol{\Pi}_{\mu\mu}(\boldsymbol{q},\Omega)\) is the corresponding diagonal element of the self-energy. This is the spectrum in the so called no mode-mixing approximation. At this level, the single-mode spectral functions resemble Lorentzian functions, but they are not true Lorentzians as they have kind of frequency-dependent center and width. As a matter of fact, in general, the spectrum of a mode can be very different from a true Lorentzian function, meaning that the quasiparticle picture for that mode is not appropriate. However, there are cases where the interaction between the SCHA phonons does not affect the quasiparticle picture but causes only a shift in the quasiparticle energy and the appearance of a finite linediwth (i.e. finite lifetime) with respect to the non-interacting case. In that case, we can write the spectral function of the mode as a true Lorentzian, Eq.(81),
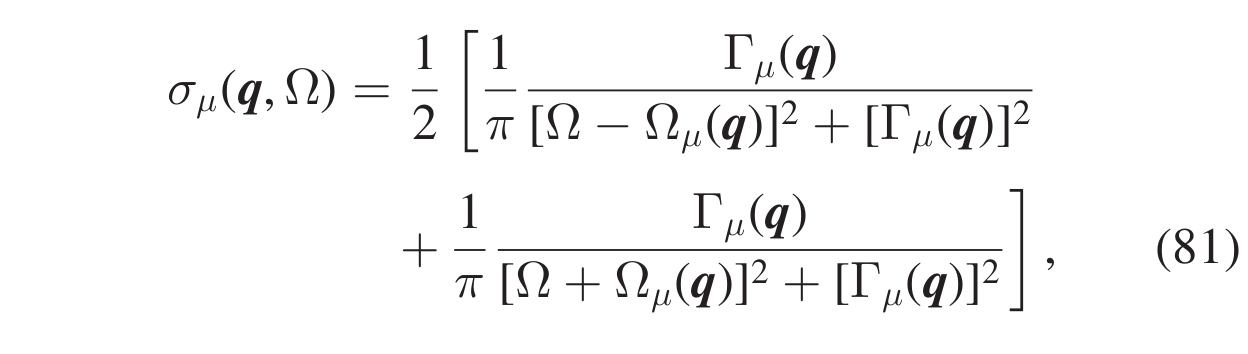
i.e., the SCHA phonon \((\boldsymbol{q},\mu)\) is a quasiparticle with definite energy \(\Omega_{\mu}(\boldsymbol{q})\) ( \(\Delta_{\mu}(\boldsymbol{q})=\Omega_{\mu}(\boldsymbol{q})-\omega_{\mu}(\boldsymbol{q})\) is called the energy shift) and lifetime \(\tau_{\mu}(\boldsymbol{q})=1/2\Gamma_{\mu}(\boldsymbol{q})\), where \(\Gamma_{\mu}(\boldsymbol{q})\) is the Lorentzian half width at half maximum (HWHM). The quantities \(\Omega_{\mu}(\boldsymbol{q})\) and \(\Gamma_{\mu}(\boldsymbol{q})\) satisfy the relations given in Eqs.(82),(83)
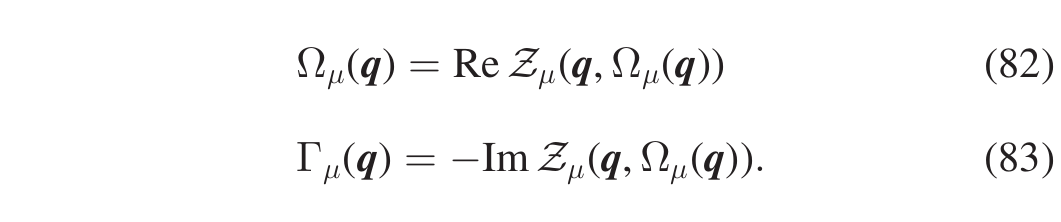
Notice that the first one is a self-consistent equation. Instead of solving the self-consistent equation to evaluate \(\Omega_{\mu}(\boldsymbol{q})\) two approximated approaches can be adpoted, both implemented in the SSCHA. One, that we call “one-shot”, evaluates the r.h.s of Eq.(82) at the SCHA frequency (Eqs.(84))
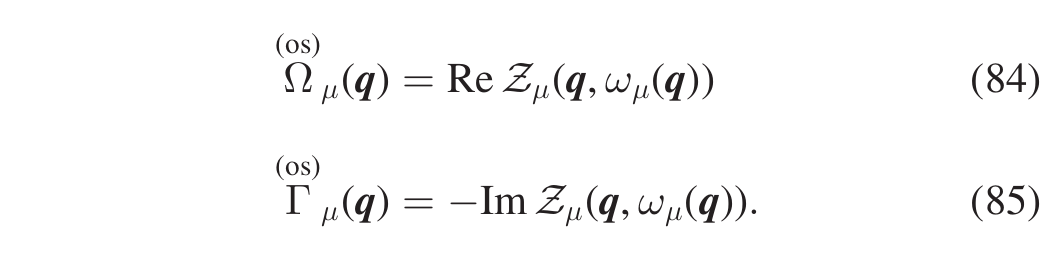
This approximation is reasonable as long as the energy shift \(\Delta_{\mu}(\boldsymbol{q})=\Omega_{\mu}(\boldsymbol{q})-\omega_{\mu}(\boldsymbol{q})\) is small. In particular, this is true if the SCHA self-energy is a (small) perturbation of the SCHA free propagator (not meaning that we are in a perturbative regime with respect to the harmonic approximation). In thas case, perturbation theory can be employed to evaluate the spectral function. If in Eq.(80) we keep only the first-order term in the self-energy, we get Eqs.(86),(87):
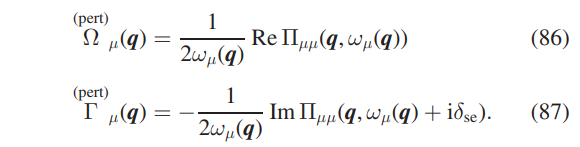
This concludes the overview on the quantities that we are going to compute for PbTe.
Calculations on PbTe
We will perform calculations on PbTe in the rock-salt structure and, in order to speed-up the calculation, we will employ the force-field model already used in previous tutorials (the force-field model can be downloaded and installed from here https://github.com/SSCHAcode/F3ToyModel). The calculations that we are going to perform are heavily underconverged and have to be consiered just as a guide to use of the SSCHA code. We will use a 2x2x2 supercell for PbTe. In order to define the force-field model on this superell we need three FCs, PbTe.ff.2x2x2.dyn1, PbTe.ff.2x2x2.dyn2, and PbTe.ff.2x2x2.dyn3
First, we need to do the SSCHA minimization. Create a directory minim, and go into it. We take the force-field FCs as starting point of the SSCHA mnimization too, with this input file min.py
import cellconstructor as CC
import cellconstructor.Phonons
import fforces as ff
import fforces.Calculator
import sscha, sscha.Ensemble, sscha.SchaMinimizer
import sscha.Relax, sscha.Utilities
# ========================= TOY MODEL DEFINITION ===========================
# Dynamical matrices that set up the harmonic part of the force-field
ff_dyn_name="04_spectral_calculations/toy_matrices_2x2x2/PbTe.ff.2x2x2.dyn"
# Paramters that set up the anharmonic part of the force-field
p3 = -0.01408
p4 = -0.01090
p4x = 0.00254
# ====================================================================
# ==========================================================
# dynamical matrices to be used as starting guess
dyn_sscha_name="04_spectral_calculations/toy_matrices_2x2x2/PbTe.ff.2x2x2.dyn"
# temperature
T=300
# minimization parameters
N_CONFIGS = 50
MAX_ITERATIONS = 10
# ====================================================================
# Setup the harmonic part of the force-field
ff_dynmat = CC.Phonons.Phonons(ff_dyn_name, 3)
ff_calculator = ff.Calculator.ToyModelCalculator(ff_dynmat)
# Setup the anharmonic part of the force-field
ff_calculator.type_cal = "pbtex"
ff_calculator.p3 = p3
ff_calculator.p4 = p4
ff_calculator.p4x = p4x
# Load matrices
dyn_sscha=CC.Phonons.Phonons( dyn_sscha_name,3)
dyn_sscha.Symmetrize()
# Generate the ensemble
supercell=dyn_sscha.GetSupercell()
ens = sscha.Ensemble.Ensemble(dyn_sscha, T, supercell)
ens.generate(N_CONFIGS)
# Compute energy and forces for the ensemble elements
ens.get_energy_forces(ff_calculator , compute_stress = False)
# Set up minimizer
minimizer = sscha.SchaMinimizer.SSCHA_Minimizer(ens)
# Ignore the structure minimization (is fixed by symmetry)
minimizer.minim_struct = False
# max number steps (negative infinite)
minimizer.max_ka=-1
# Setup the minimization parameter for the covariance matrix
minimizer.set_minimization_step(1.0)
# Setup the threshold for the ensemble wasting
minimizer.kong_liu_ratio =0.8 # Usually 0.5 is a good value
minimizer.meaningful_factor=1e-5 # meaningul factor
# Initialize the simulation
relax = sscha.Relax.SSCHA(minimizer,
ff_calculator,
N_configs = N_CONFIGS,
max_pop = MAX_ITERATIONS)
# Define the I/O operations
# To save info about the free energy minimization after each step
ioinfo = sscha.Utilities.IOInfo()
ioinfo.SetupSaving("minim_info")
relax.setup_custom_functions(custom_function_post = ioinfo.CFP_SaveAll)
# Start the minimization
relax.relax()
# Print in stdout the info about the minimization
# and save the final dynamical matrix
relax.minim.finalize()
relax.minim.ensemble.save_bin("./data_pop", population_id=1)
relax.minim.dyn.save_qe("SSCHA.T{}.dyn".format(T))
launching
$ python min.py > min.out
after a few second the minimization has concluded. The three SSCHA FCs matrices have been saved as SSCHA.T300.dyn#q. Now we need to compute the third order FCs (FC3s) (and the Hessian FCs). At the end of the SSCHA minimization, we saved the last population and the dynamical matrices that generated it too. Using them, we compute the Hessian matrices and the FC3s. Exit from minim, create a directory hessian, go into it, and use this input file hessian.py
import cellconstructor as CC
import sscha.Ensemble
#
NQIRR = 3
Tg = 300
T = 300
#
pop_dyn = CC.Phonons.Phonons('minim/data_pop/dyn_gen_pop1_', 3)
sscha_dyn = CC.Phonons.Phonons('minim/SSCHA/SSCHA.T300.dyn', 3)
#
ens = sscha.Ensemble.Ensemble(pop_dyn, Tg)
ens.load_bin('minim/data_pop', population_id = 1)
ens.update_weights(sscha_dyn, T)
#
hessian_dyn, d3 = ens.get_free_energy_hessian(include_v4 = False,
return_d3 = True)
hessian_dyn.save_qe('Hessian.dyn')
############################### FC3 part #############################################
tensor3 = CC.ForceTensor.Tensor3(dyn=sscha_dyn) # initialize 3rd order tensor
tensor3.SetupFromTensor(d3) # assign values
tensor3.Center() # center it
tensor3.Apply_ASR() # apply ASR
tensor3.WriteOnFile(fname="FC3",file_format='D3Q') # write on file
giving
$ python hessian.py > hessian.out
We already did an Hessian calculation in a previous tutorial. The new part is the creation of the 3rd order FCs (FC3s), which we wrote in the file FC3. Some comments about the input file. In get_free_energy_hessian we set return_d3 = True because we need these informations to set up the FC3s. Moreover, since we are not going to use forth order FCs (we will work within the “bubble approximation”), we set include_v4 = False, which in general saves a lot of computation time. Before writing the FC3s on file, we center it (a step necessary to perform Fourier interpolation), and apply the acoustic sum rule (ASR), since the centering spoils it.s
The format chosen here to write the FC3 file is the same used in the d3q.x code https://anharmonic.github.io/d3q/. To be precise: exploiting the lattice translation symmetry, the third order FCs can be written as \(\Phi^{\alpha_1,\alpha_2,\alpha_3}_{a_1 a_2 a_3}(0,\boldsymbol{R},\boldsymbol{S})\), where \(\alpha_1,\alpha_2,\alpha_3\) are cartesian indices, \(a_1, a_2, a_3\) atomic indices in the unit cell, and \(\boldsymbol{R},\boldsymbol{S}\) lattice vectors. The FC3 file in D3Q format is
alpha_1 alpha_2 alpha_3 at_1 at_2 at_3
N_RS
R_x R_y R_z S_x S_y S_z phi(alpha_1,at_1,alpha_2,at_2,alpha_3,at_3)
...
alpha_1 alpha_2 alpha_3 at_1 at_2 at_3
N_RS
R_x R_y R_z S_x S_y S_z phi(alpha_1,at_1,alpha_2,at_2,alpha_3,at_3)
...
For each alpha_1 alpha_2 alpha_3 at_1 at_2 at_3 we have a block where: the first line is N_RS, which is
the number of \(\boldsymbol{R},\boldsymbol{S}\) considered. Each subsequent line refers to a couple \(\boldsymbol{R},\boldsymbol{S}\), with R_x R_y R_z and S_x S_y S_z the crystal coordinates of \(\boldsymbol{R}\) and \(\boldsymbol{S}\), respectively, and phi(alpha_1,at_1,alpha_2,at_2,alpha_3,at_3) the corresponding FCs value \(\Phi^{\alpha_1\alpha_2\alpha_3}_{a_1 a_2 a_3}(0,\boldsymbol{R},\boldsymbol{S})\).
Equipped with the third order SSCHA FCs ,written in real space in the FC3 file, and the second-order SSCHA FCs, written in reciprocal space in the SSCHA.T300.dyn#q files, we have all the ingredient to compute the spectral functions. As first calculation, we compute the spectral function using Eq.(70) but within the “static approximation”, this meaning that we keep the selfenergy blocked with \(\Omega=0\), as shown in Eq.(66) (within the bubble approximation)
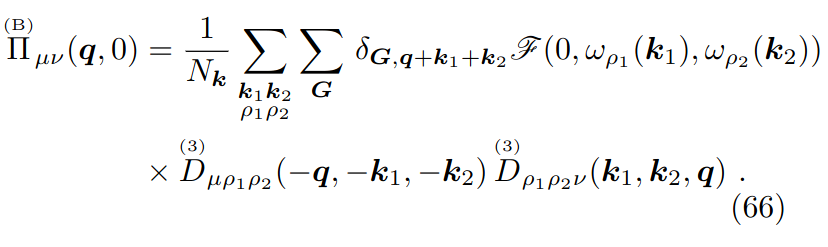
In order to do that, exit from the current directory hessian, create a directory spectral_static, enter into it, and use this input file spectral_static.py to compute the spectral function in the static approximation, for the special point \(X\)
import cellconstructor as CC
import cellconstructor.ForceTensor
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3)
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
# integration grid
k_grid=[2,2,2]
# X in 2pi/Angstrom
points=[0.0,-0.1547054, 0.0]
CC.Spectral.get_full_dynamic_correction_along_path(dyn=dyn,
tensor3=FC3,
k_grid=k_grid,
e1=100, de=0.1, e0=0, # energy grid
T=300,
q_path=points,
static_limit = True,
filename_sp='full_spectral_func_X')
We used as integration \(\boldsymbol{k}\)-grid (i.e. the \(\boldsymbol{k}\)-grid of the summation in Eqs.(66), (75)) the grid commensurate with the supercell, i.e. a 2x2x2 grid. In that case, using the centering is irrelevant, as there is no Fourier interpolation. With
$ mpirun -np 4 python spectral_static.py > spectral_static.out
we run the code with MPI with 4 parallel processes. In output we have the file full_spectral_func_X_static.dat that contains the spectral function
# -------------------------------------------------------------
# len (2pi/Angstrom), energy (cm-1), spectral function (1/cm-1)
# -------------------------------------------------------------
0.000000 0.0000000 0.0000000
0.000000 0.1000000 0.0000000
0.000000 0.2000000 0.0000000
0.000000 0.3000000 0.0000001
0.000000 0.4000000 0.0000002
0.000000 0.5000000 0.0000003
...
where the first line indicates the lenght of the path. This would be relevant in case we had not just a single \(\boldsymbol{q}\) point, but a path of \(\boldsymbol{q}\)-points. In that case, we would have several blocks, one for each \(\boldsymbol{q}\) point, and the first column of each block would indicate the lenght of the \(\boldsymbol{q}\)-path. In this case, since we have just one point, we have just one block with the first column equal to zero. Plotting the 3rd vs 2nd column we obtain this result:
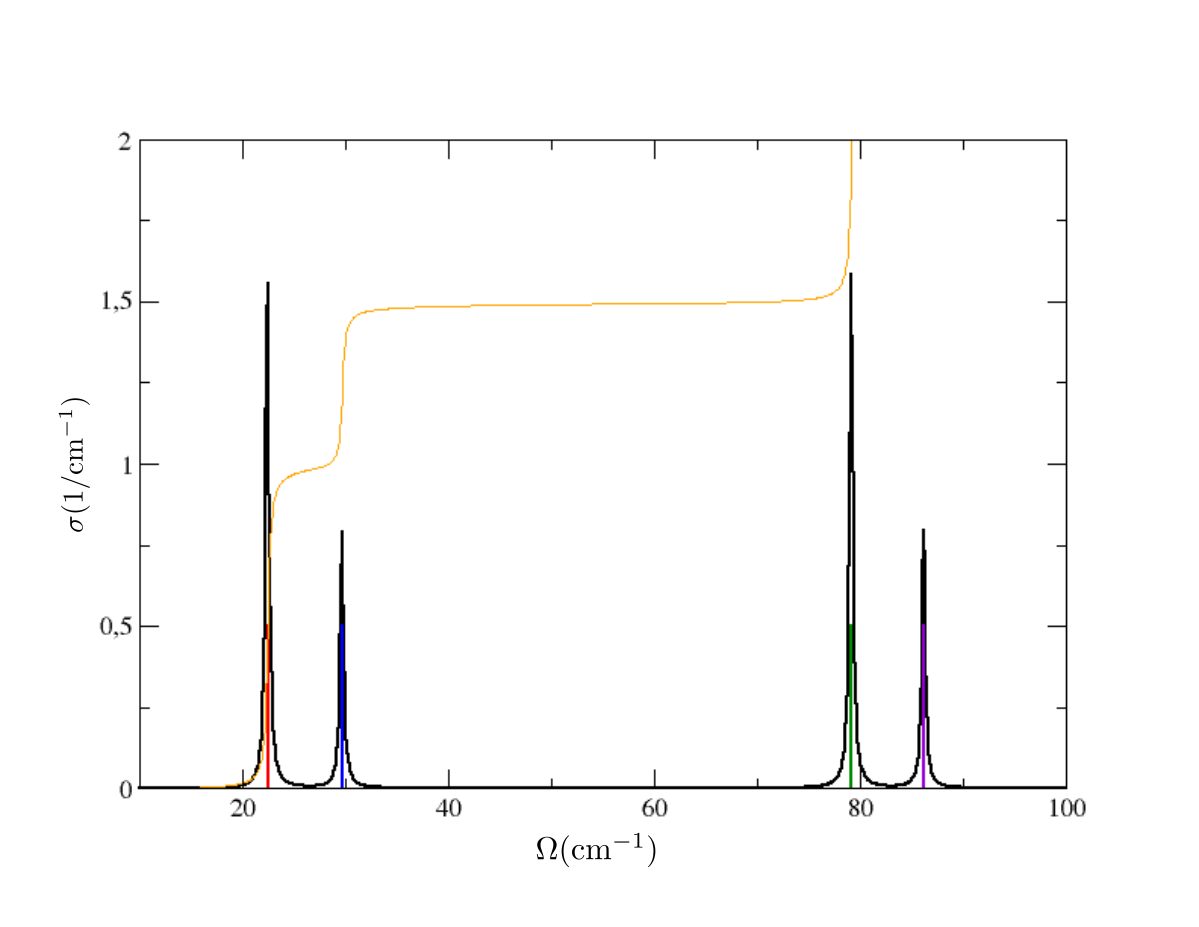
We have Dirac deltas ( to be precise, extremely narrow Lorentzians whose width is given only by the choice of the finite size of the used energy grid) around values that coincides with the Hessian frequency values (plotted here with vertical lines), that you can find in the Hessian.dyn3 file obtained in the previous run. Indeed, the Hessian calculation corresponds exactly to a calculation done with the static self-energy. Two observations. The height of the spikes is proportional to the degeneracy of the modes. The yellow line indicates the integral function \(\int_0^{\Omega}\sigma(\Omega',\boldsymbol{q})\,d\Omega'\), which at the end returns the value: [number of modes]/2 (therefore 3 in this case). This is a general sum rule fulfilled by the spectral function (not only in the static approximation).
Now we do a full calculation (no static approximation anymore). In this case, we need to specify the smearing parameter \(\delta_{\scriptscriptstyle{\text{se}}}\) to compute the dynamic selfenergy from Eq.(75). In order to be tidy, let us do this calculation in another directory spectral (and let us do the same for all the subsequent calculations, new calculations in new directories). Using this spectral.py input file
import cellconstructor as CC
import cellconstructor.ForceTensor
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3)
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
# integration grid
k_grid=[20,20,20]
# X in 2pi/Angstrom
points=[0.0,-0.1547054, 0.0]
CC.Spectral.get_full_dynamic_correction_along_path(dyn=dyn,
tensor3=FC3,
k_grid=k_grid,
e1=100, de=0.1, e0=0, # energy grid
sm1=10.0,sm0=1.0,nsm=3, # smearing values
T=300,
q_path=points,
static_limit = True,
filename_sp='full_spectral_func_X')
where now we have specified that we want to do the calculation with 3 smearing values (equally spaced) between 1.0 and 10.0 cm-1 (thus we will have 1.0, 5.5, and 10.0 cm-1) With
$ mpirun -np 4 python spectral.py > spectral.out
in output we have three files with the spectral functions, one for each smearing value. In general, convergence must be studied with respect to the integration \(\boldsymbol{k}\)-grid and smearing used. Plotting the static result and the dynamic result for sm=1.0 cm-1, both computed with 20x20x20 \(\boldsymbol{k}\)-grid, we see this result
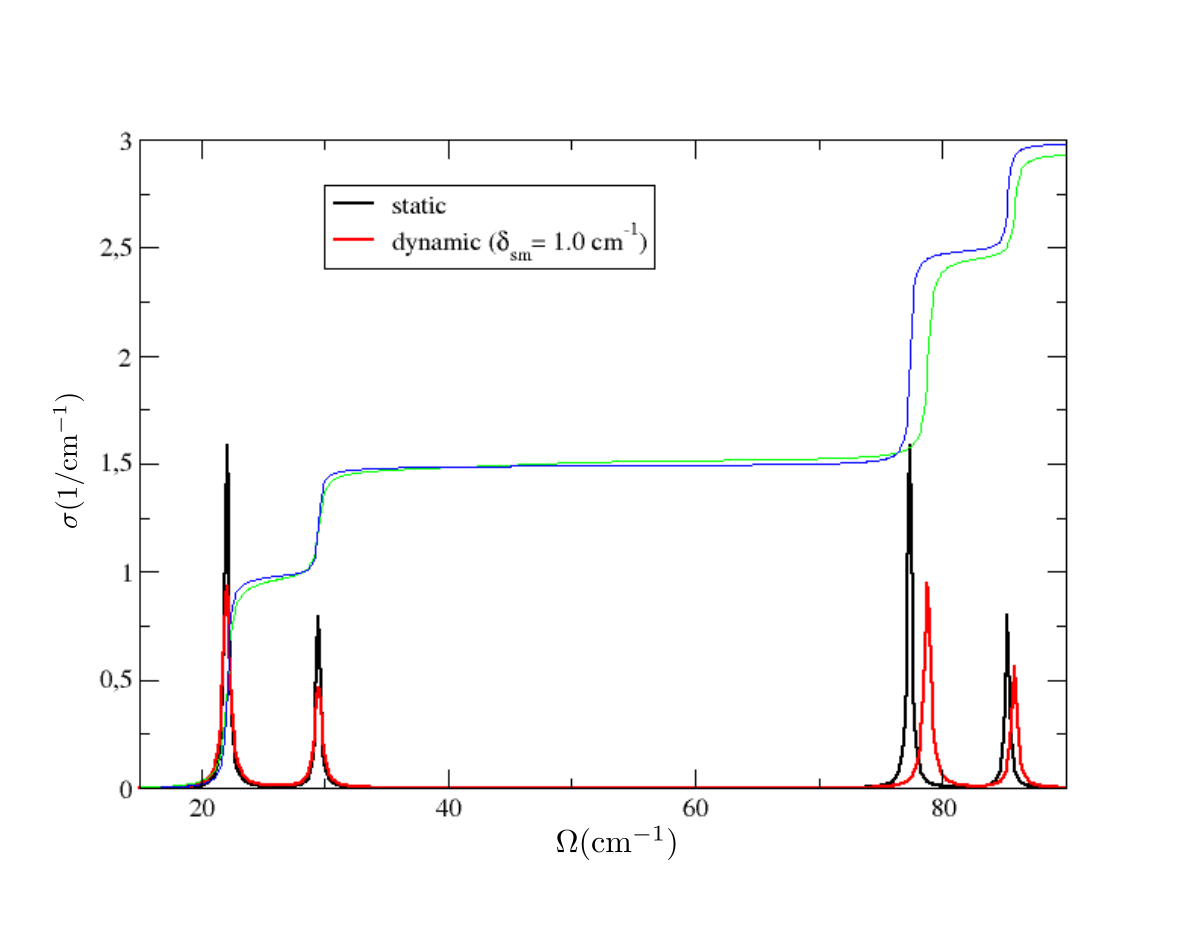
Therefore, we can conclude that in \(X\) the SSCHA phonons are barely affected by the interaction. However, the situation is different if analogous calculation is done in \(\Gamma\).
Exercise
In \(\Gamma\), do the same calculations previously done in \(X\), and plot the results
This is the result you should obtain
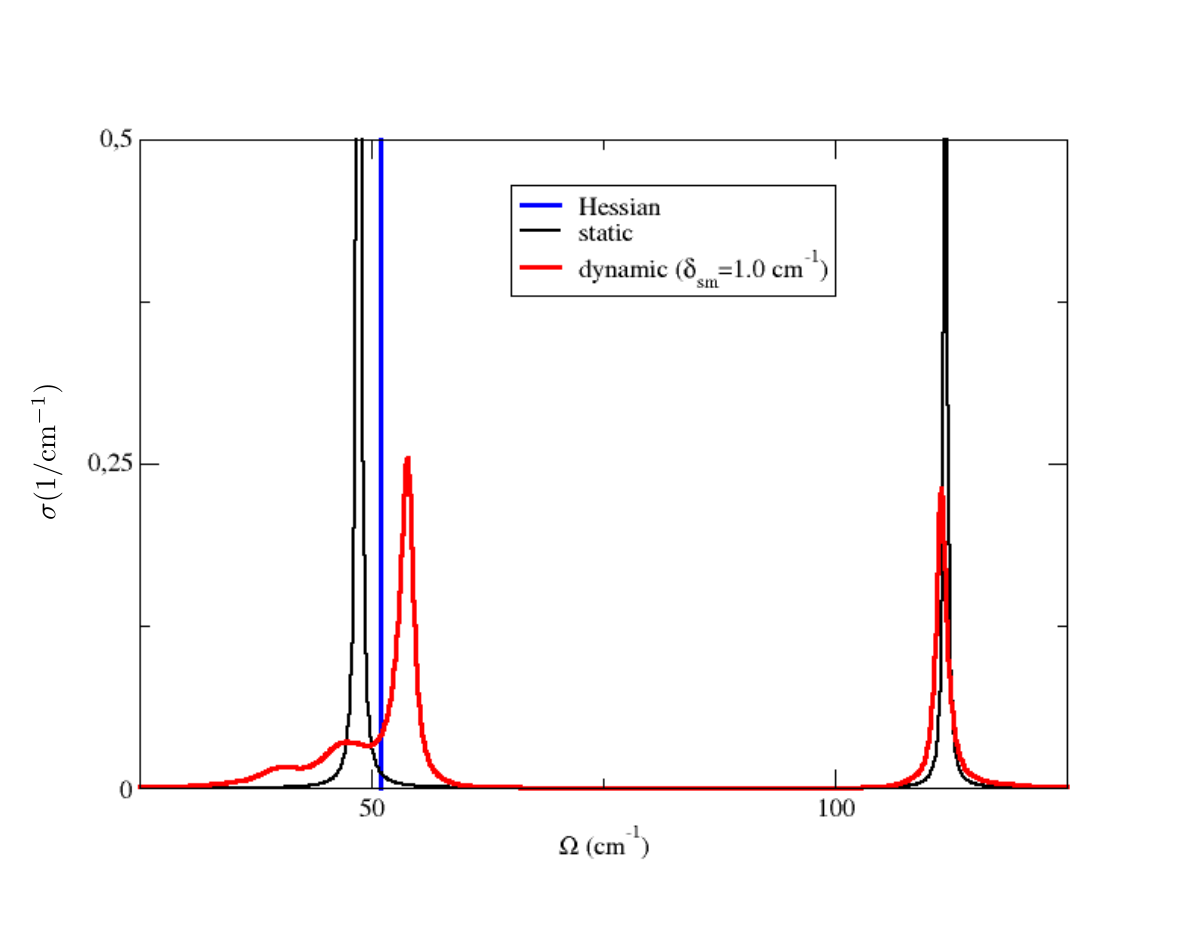
Notice that here the triple-degenerate optical mode of the Hessian dynamical matrix is splitted into due different peaks of the static spectral function (LO and double degenerate TO). This is due to the LO-TO splitting occurring in PbTe. The frequencies in the Hessian dynamical matrix in \(\Gamma\) refer only to the short-range part of the FCs. However, the long-range dipole-dipole contribution coming from the Effective Charges (nonanalytic contribution), which is at the origin of the LO-TO splitting, is taken into account when the spectral function is computed. Moreover, notice that when dynamic spectral function is considered, the double-degenerate TO mode gets smeared, showing a strong non-Lorentzian character. When 4x4x4 supercell calculations are performed, it clearly appears a satellite peak.
Before continuing the spectral analysis, let us spend some time to investigate the static correction. As said, the static spectral function is nothing but a collection of Dirac-deltas centered around the Hessian eigenvalues. Therefore, in the static case the only information are the eigenvalues, there is not a complex spectrum to be analyzed. Indeed, there is a routine that we can use to compute the static correction for any q point, and for any integration grid. With this input file static.py
import cellconstructor.ForceTensor
import cellconstructor as CC
import numpy as np # will be used just to create a path
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3) # SSCHA matrices
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
# integration grid
k_grid=[4,4,4]
Xcoord=0.1547054
points=[[0.0,z,0.0] for z in np.linspace(-Xcoord,Xcoord,100)] # create the path
# you can also download the path from a file
CC.Spectral.get_static_correction_along_path(dyn=dyn,
tensor3=FC3,
k_grid=k_grid,
T=300,
q_path=points)
with
$ mpirun -np 4 python static.py > static.out
we obtain the file v2+d3static_freq.dat, done like this
# ------------------------------------------------------------------------
# len (2pi/Angstrom), sscha freq (cm-1), sscha + static bubble freq (cm-1)
# ------------------------------------------------------------------------
0.000000 22.6699858 22.6699858 ... 22.1602770 22.1717260 ...
0.003125 22.7847829 22.7847829 ... 29.9763683 80.8414572 ...
...
where the first column is the lenght of the path in 2:math:pi/Angstrom, the next (6, in this case) columns are the SSCHA frequencies, and the next (6, in this case) columns are the SSCHA+static bubble self-energy-corrected frequencies. This is the plot obtained with this result
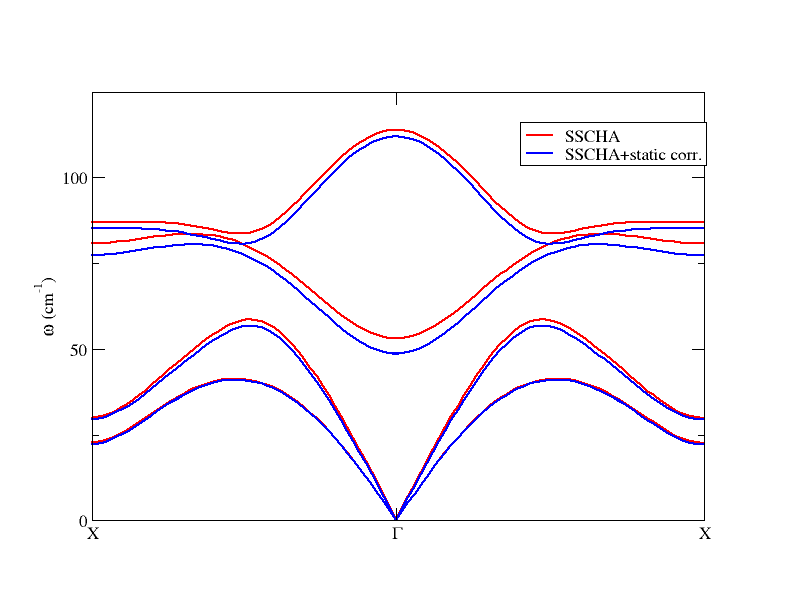
Therefore, as long as one is interested only in the static correction, e.g. because one wants to study the structural instability,
the routine get_static_correction_along_path is the one that has to be employed. Indeed, notice that this is the proper way to
detect instabilities (imaginary frequencies) in points of the Brillouin zone that do not belong to the grid used to compute the Hessian.
One should not Fourier interpolate the Hessian matrices computed on a grid, in order to obtain the frequency dispersion along a path, but rather should interpolate the correction
and add it to the SSCHA frequency, point by point (which is what we are doing here). Moreover, in this way we can increase the integration \(k\)-grid to reach the convergence. Notice that the LO-TO splitting has been properly taken into account.
We can now go back to the spectral calculations. In general, calculations done with Eq.(70) can be heavy, but often the off-diagonal terms of the phonon self-energy in the mode basis set can be neglected and use Eqs. (78), (79), (80). This is the case of PbTe. With this input file nomm_spectral.py
import cellconstructor as CC
import cellconstructor.ForceTensor
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3)
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
# integration grid
k_grid=[20,20,20]
G=[0.0,0.0,0.0]
points=G
CC.Spectral.get_diag_dynamic_correction_along_path(dyn,
tensor3=FC3,
k_grid=k_grid,
e1=150, de=0.1, e0=0.0,
sm1=1.0, sm0=1.0,
nsm=1,
q_path=points,
T=300.0)
and
$ mpirun -np 4 python nomm_spectral.py > nomm_spectral.out
we obtain several files:
spectral_func_1.00.dat
with the structure
# --------------------------------------------------------------------------------- # len (2pi/Ang), ene. (cm-1), spec. func. (1/cm-1), spec. fun. mode comp. (1/cm-1) # --------------------------------------------------------------------------------- 0.000 0.000 0.000 -0.000 0.000 ... 0.000 0.100 1.527 0.509 0.509 ... 0.000 0.200 2.387 0.795 0.795 ... ...
The file is made by several blocks, one for each \(\boldsymbol{q}\) point of the path considered (now we have just one point, thus one block). The first column of the block gives the length of the path (at that point). The second and third column give the energy and total spectrum, respectively. The subsequent columns give the contribution to the spectrum given by each mode (Cfr. Eqs.(78),(79)). Plotting the 3rd vs 2nd column you can verify that in this case the spectrum is essentially identical to the one already obtained with the full formula (i.e. to the spectrum obtained considering the off-diagonal terms of the self-energy too). Notice that in this file we have the spectrum given by the three acoustic modes in \(\Gamma\). We did not consider the translational modes (because trivial) in the calculation done with get_full_dynamic_correction_along_path, where the flag
notranslby default was set equal toTrue.spectral_func_lorentz_one_shot_1.00.dat, spectral_func_lorentz_perturb_1.00.dat
These files have the same structure of spectral_func_1.00.dat. However, now the spectral functions are computed in the Lorenztian approximation, Eq.(81), using the one-shot, Eqs.(84),(85) and the perturbative, Eqs.(86),(87), values of the energy and HWHM. The codes offers also the possibility to use a still very tentative approach to solve the self-consistent relation Eqs.(82),(83), and produce the relative Lorentzian spectral functions. Plotting the spectral functions of the TO mode from spectral_func_1.00.dat and spectral_func_lorentz_one_shot_1.00.dat we obtain this
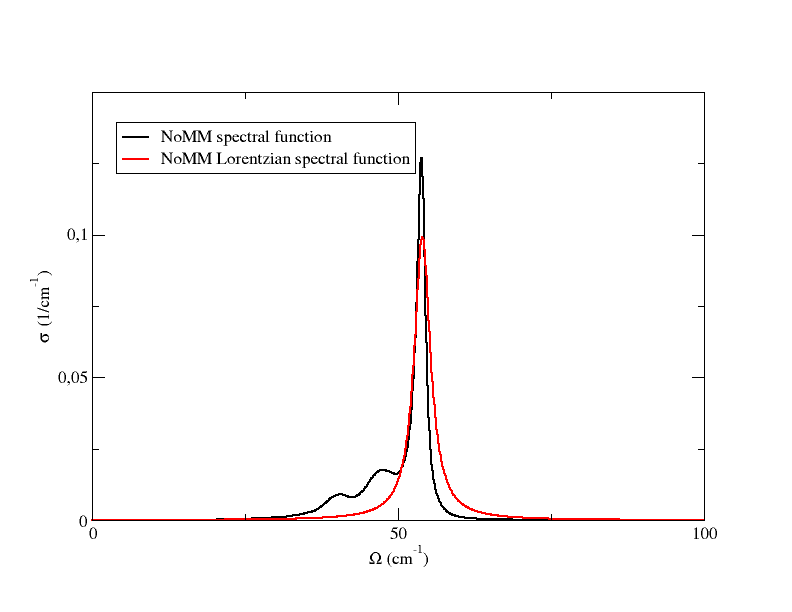
This confirms the strong non-Lorentzian character of this mode
v2_freq_shift_hwhm_one_shot_1.00.dat, v2_freq_shift_hwhm_perturb_1.00.dat
They have the structure
# ----------------------------------------------------------------- # len (2pi/Angstrom), SSCHA freq (cm-1), shift (cm-1) , HWHM (cm-1) # ----------------------------------------------------------------- ....
For each \(\boldsymbol{q}\) point there is a line, with the lenght along the path, the SSCHA frequencies for that point, \(\omega_{\mu}(\boldsymbol{q})\), the energy shift \(\Delta_\mu(\boldsymbol{q})=\Omega_\mu(\boldsymbol{q})-\omega_\mu(\boldsymbol{q})\) and the HWHM \(\Gamma_\mu(\boldsymbol{q})\).
freq_dynamic_one_shot_1.00.dat, freq_dynamic_perturb_1.00.dat
They have the structure
# ------------------------------------------------------------ # len (2pi/Angstrom), SSCHA+shift (sorted) (cm-1), HWHM (cm-1) # ------------------------------------------------------------ ....
For each \(\boldsymbol{q}\) point there is a line, with the lenght along the path, the shifted frequencies \(\Omega_\mu(\boldsymbol{q})=\omega_\mu(\boldsymbol{q})+\Delta_\mu(\boldsymbol{q})\) (sorted in incresing value, in principle different from the SSCHA-frequency increasing order) and the corresponding HWHMs \(\Gamma_\mu(\boldsymbol{q})\). This is the file that has to be used to plot the correct phonon dispersion, together with the linewidth.
There is a dedicated routine to compute, with less computational time and more accuracy, only the energy shift (i.e. the corrected frequency) and the linewidth of the modes in the one-shot and perturbative no-mode-mixing Lorentzian approach. It is the get_os_perturb_dynamic_correction_along_path routine, using the
os_perturb_correction.py input file
import cellconstructor as CC
import cellconstructor.ForceTensor
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3)
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
# integration grid
k_grid=[10,10,10]
points=[0.0,0.0,0.0]
CC.Spectral.get_os_perturb_dynamic_correction_along_path(dyn,
tensor3=FC3,
k_grid=k_grid,
sm1=1.0, sm0=1.0,
nsm=1,
q_path=points,
T=300.0)
Exercise
Do this calculation to obtain the dispersion along the path \(X-\Gamma-X\).
After that, using this script to extract the results
for i in `seq 1 6`
do
awk -v i="${i}" '{ if ( NR > 3 ) printf"%22.11f%22.11f%22.11f%22.11f\n", \
$1,$(i+1),$(i+1)+$(i+7),$(i+1)-$(i+7)}' freq_dynamic_1.0.os.dat > freq_${i}
done
and then using this gnuplot script plot.gp
set terminal pngcairo size 2048,1536 enhanced
set output 'freq.png'
xmin=0
xmax=0.30941100000
set xrange[xmin:xmax]
set multiplot
set object rectangle from graph 0,0 to graph 1,1 \
behind fillcolor rgb 'black' fillstyle transparent solid 0.100 noborder
plot for [i=1:6] 'freq_'.i using 1:3:4 with filledcurves \
fs transparent solid 0.125 noborder lc rgb "blue" notitle
plot for [i=1:6] 'freq_'.i using 1:2 with lines \
lc rgb "black" lw 3.5 notitle
$ gnuplot plot.gp
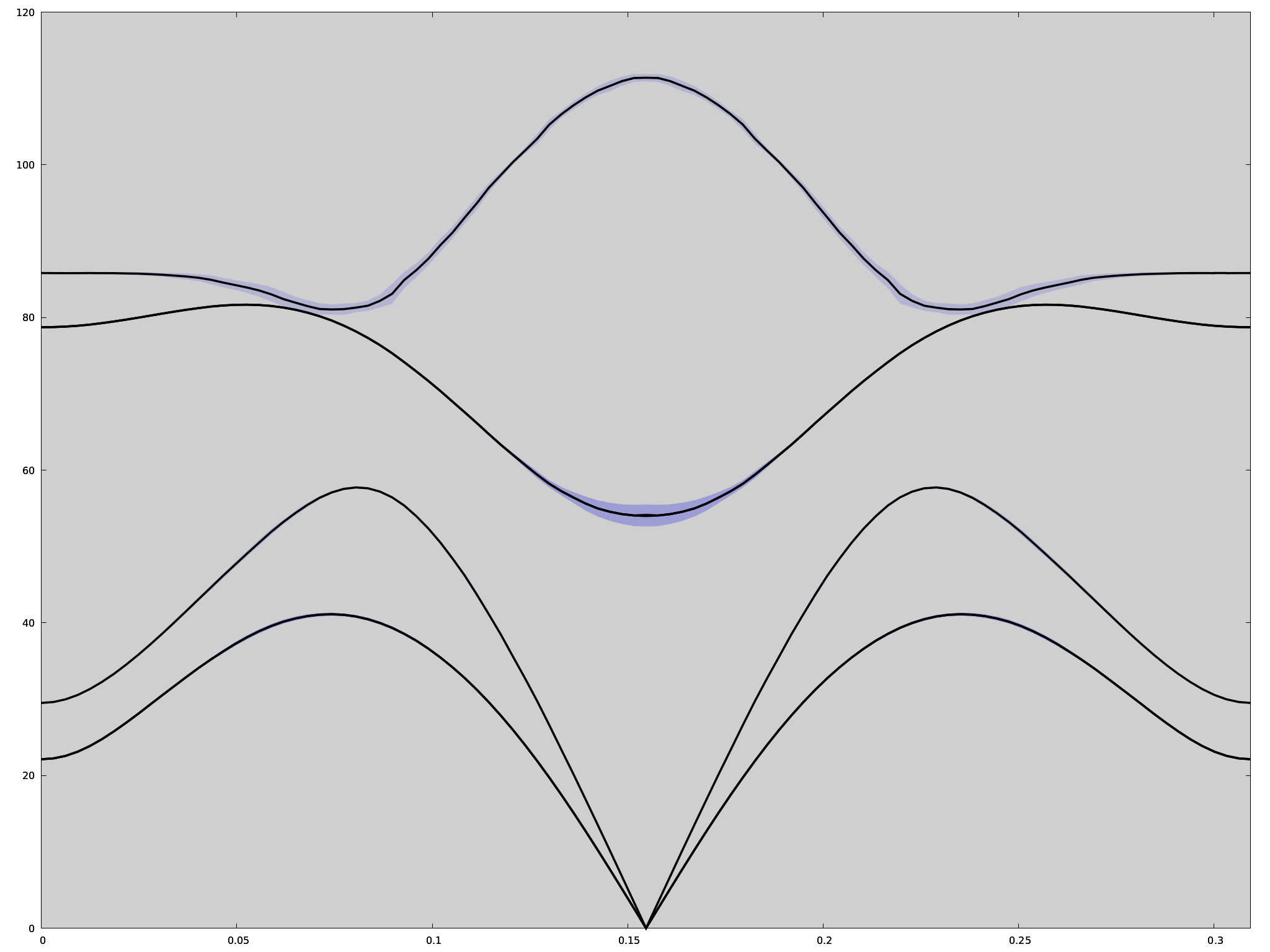
you obtain this figure
Here you have the plot of the shifted SSCHA phonon frequencies with the linewidth. However, it must be remembered that this picture is appropriate as long as the Lorentzian picture is valid. We already know that at least in \(\Gamma\) this is not really the case (as said, this is even more evident if the calculation is done with a 4x4x4 supercell). In that case, the best thing to do is a spectral calculation (full, or in the no-mode-mixing approximation), and use the three columns (lenght of the path & energy & spectral value) to do a colorplot. For example, this is the kind of result that you obtain for PbTe with the 4x4x4 supercell
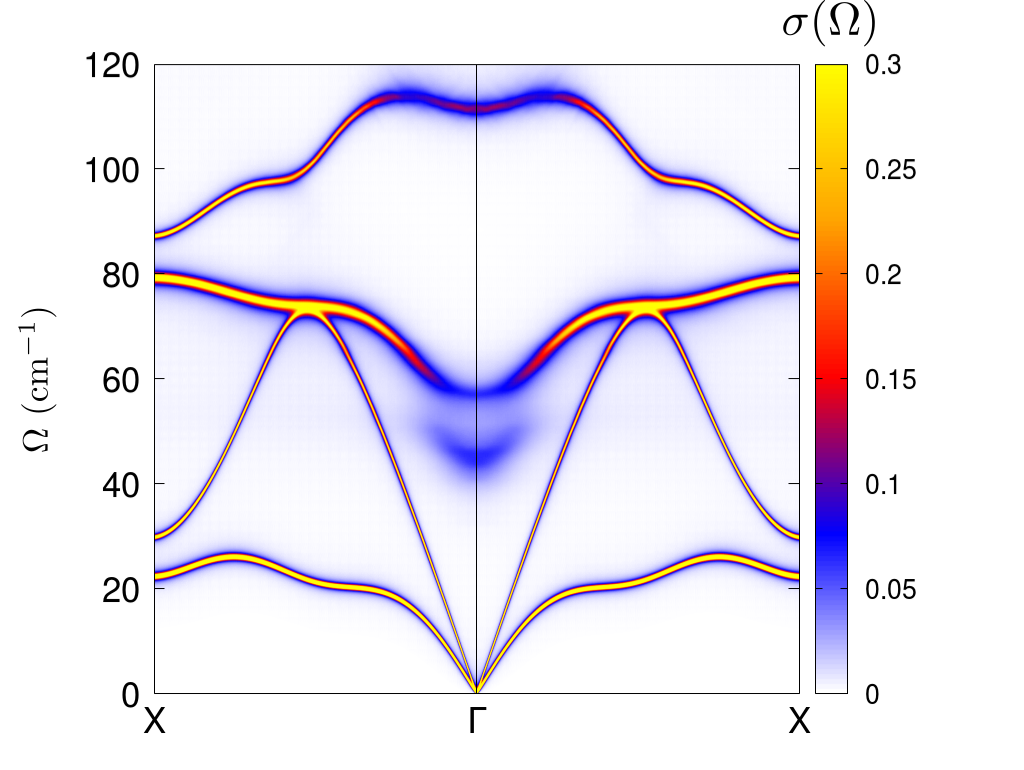
Exercise
Do the no-mode-mixing calculation along the path \(X-\Gamma-X\) with smearing \(10.0\,\text{cm}^{-1}\)
We conclde this tutorial stressing that a convergence analysis in terms of integration grid and smearing has to be done in order to obtain reliable results. The get_os_perturb_dynamic_correction_along_path routine is the best tool to do that. With this input.py input file you can do
the calculation for several integration grids
import cellconstructor as CC
import cellconstructor.ForceTensor
dyn = CC.Phonons.Phonons("minim/SSCHA.T300.dyn",3)
FC3 = CC.ForceTensor.Tensor3(dyn=dyn)
FC3.SetupFromFile(fname="hessian/FC3",file_format='D3Q')
for kval in [4,8,16,32]:
print("COMPUTING {}".format(kval))
CC.Spectral.get_os_perturb_dynamic_correction_along_path(dyn,
tensor3=FC3,
k_grid=[kval,kval,kval],
sm1=20.0, sm0=0.1,
nsm=80,
q_path=[0.0,0.0,0.0],
T=300.0,
filename_shift_lw = 'shift_hwhm_{}'.format(kval),
filename_freq_dyn = 'freq_{}'.format(kval))
giving
$ mpirun -np 4 python input.py > output
From output you can take the list of smearing values and write them in a file sm.dat. After that, you can collect the results with this extract.sh script
for grid in 4 8 16 32
do
> ${grid}x${grid}x${grid}.dat
while read sm
do
tail -1 shift_hwhm_${grid}_${sm}.os.dat \
| awk -v sm="${sm}" '{printf"%11.7f\t%22.11f\n",sm,$(NF-1)}' \
>> ${grid}x${grid}x${grid}.dat
done < sm.dat
done
giving
$ bash extract.sh
so as to obtain the files 4x4x4.dat, 8x8x8.dat, 16x16x16.dat, and 32x32x32.dat. Plotting them you obtain
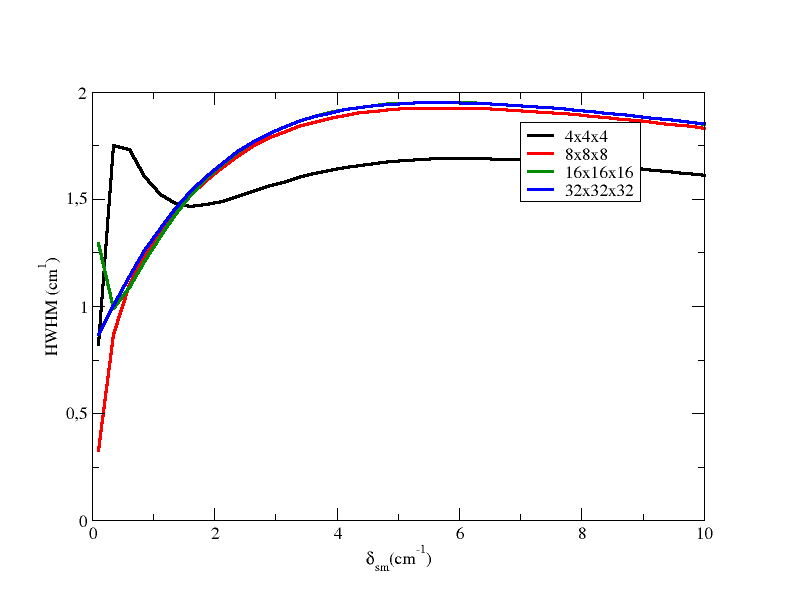
From the plot, you can see that you need at least a 8x8x8 grid to obtain a converged value, using smearing equal to 1.0 cm-1.