This tutorial was prepared for the 2023 SSCHA School by Lorenzo Monacelli. You can see here the video os the hands-on session:
The material needed for this tutorial can be downloaded here.
In the previous tutorial, you learned how to compute the spectral function by integrating the bubble in the Fourier space, with the dynamical ansatz formulated by Bianco et al, Physical Review B, 96 , 014111, 2017. Instead, we will employ the Lanczos algorithm within the Time-Dependent Self-Consistent Harmonic Approximation (TD-SCHA) Monacelli, Mauri, Physical Review B 103, 104305, 2021.
For this reason, we need the package tdscha (it is suggested to configure it with the Julia speedup to run faster, see the installation guide).
Computing the IR signal in ICE
We use an ensemble already computed of the phase XI of ice (low-temperature ice ad ambient pressure and prototype of standard cubic ice) to get the IR spectrum.
Inside the directory data, we find an already calculated ensemble of ice XI at 0K with the corresponding original dynamical matrix start_dyn_ice1 employed to generate the ensemble and the dynamical matrix final_dyn_ice1 after the SSCHA minimization.
An introduction
The infrared spectrum is related to the dipole-dipole response function:
where the average \(\left<M(t)M(0)\right>\) is the quantum average at finite temperature.
Exploiting the TD-SCHA formalism introduced in the previous lecture, this response function can be written as:
where \(\boldsymbol{G}(\omega)\) is the TD-SCHA green function, while the \(\boldsymbol{r}\) and \(\boldsymbol{q}\) are vectors that quantify the perturbation and response, respectively.
In particular, if we neglect two-phonon effects (nonlinear coupling with light), we get that
where \({\mathcal Z}_{\alpha a}\) is the Born effective charge of atom \(a\), with polarization \(\alpha\), and \(G_{ab}(\omega)\) is the one-phonon green function, (its imaginary part is precisely the spectral function).
Indeed, we need to compute the effective charges. This can be done directly by quantum espresso using linear response theory (ph.x).
Exercise
Use the knowledge of cellconstructor to extract a structure file from the final dynamical matrix to submit the calculation of the dielectric tensor, Effective charges, and Raman tensor in quantum espresso.
Hint. The structure is the attribute structure of the Phonons object. The structure in the SCF file can be saved with the save_scf method of the Structure object.
You can then attach the structure to the header of the espresso ir_raman_header.pwi.
Notice that we are using norm-conserving pseudo-potentials and LDA exchange-correlation functional, as the Raman Tensor in quantum espresso is implemented only with them. However, it is usually an excellent approximation. ir_raman_header.pwi.
You must run the pw.x code and the ph.x code (ir_raman_complete.phi), which performs the phonon calculation.
We provide the final output file in ir_raman_complete.pho
Prepare the infrared response
We need to attach the Raman Tensor and effective charges computed inside ir_raman_complete.pho to the final dynamical matrix, we will use this to initialize the response function calculation, as in Eq.1.
To attach the content of an espresso ph calculation (only Dielectric tensor, Raman Tensor, and Born effective charges) to a specific dynamical matrix, use
dyn.ReadInfoFromESPRESSO("ir_raman_complete.pho")
If you save the dynamical matrix in quantum espresso format, before the frequencies and the diagonalization, there will be the Dielectric tensor
Dielectric Tensor:
1.890128098000 0.000000000000 0.000000000000
0.000000000000 1.912811137000 0.000000000000
0.000000000000 0.000000000000 1.916728724000
Followed by the effective charges and the Raman tensor.
Submitting the IR calculation
With the following script, we submit a TD-SCHA calculation for the IR.
import numpy as np
import cellconstructor as CC, cellconstructor.Phonons
import sscha, sscha.Ensemble
import tdscha, tdscha.DynamicalLanczos as DL
# Load the starting dynamical matrix
dyn_start = CC.Phonons.Phonons("start_dyn_ice")
# Load the ensemble
temperature = 0 # K
population = 2
n_configs = 10000
ensemble = sscha.Ensemble.Ensemble(dyn_start, temperature)
ensemble.load("data", population, n_configs)
# Load the final dynamical matrix
final_dyn = CC.Phonons.Phonons("final_dyn_ice")
final_dyn.ReadInfoFromESPRESSO("ir_raman_complete.pho")
# Update the ensemble weights for the final dynamical matrix
ensemble.update_weights(final_dyn, temperature)
# Setup the TD-SCHA calculation with the Lanczos algorithm
lanczos = DL.Lanczos(ensemble)
lanczos.ignore_v3 = True
lanczos.ignore_v4 = True
# If you have julia-enabled tdscha installed uncomment
# lanczos.mode = DL.MODE_FAST_JULIA
# for a x10-x15 speedup.
lanczos.init()
# Setup the IR response
polarization = np.array([1,0,0]) # Polarization of light
lanczos.prepare_ir(pol_vec = polarization)
# Run the algorithm
n_iterations = 1000
lanczos.run_FT(n_iterations)
lanczos.save_status("ir_xpol")
Congratulations! You ran your first TD-SCHA calculation. You can plot the results by using:
tdscha-plot.py ir_xpol.npz
The script tdscha-plot.py is automatically installed with the tdscha package.
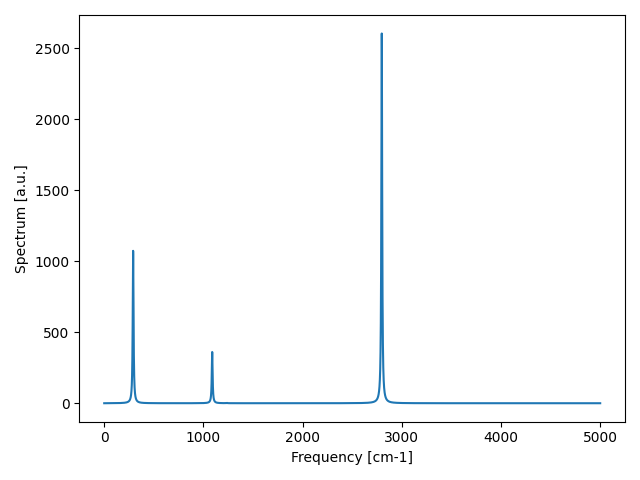
Fig. 12 IR spectrum with both include_v3 and include_v4 set to False.
Additionally, tdscha-plot.py takes three more parameters: the range of the frequencies to be displayed and the smearing.
Deep dive into the calculation
Let us dive a bit into the calculation. The beginning of the script should be almost self-explanatory, as we are just loading dynamical matrices, dielectric tensors, and effective charges.
The line
ensemble.update_weights(final_dyn, temperature)
deserves special attention. Here, we are changing the weights of the configurations inside the ensemble to simulate the specified dynamical matrix and temperature, even if they differ from those used to generate the ensemble. This is useful to compute the spectrum at several temperatures without extracting and calculating a new ensemble each time.
# Setup the TD-SCHA calculation with the Lanczos algorithm
lanczos = DL.Lanczos(ensemble)
lanczos.ignore_v3 = True
lanczos.ignore_v4 = True
lanczos.init()
Then we initialize the Lanczos algorithm for the tdscha, passing the ensemble.
The ignore_v3 and ignore_v4 are flags that, if set to True, the 3-phonon and 4-phonon scattering will be ignored during the calculation.
As you can see from the output, our IR signal had very sharp peaks because we ignored any phonon-phonon scattering process that may give rise to a finite lifetime.
By setting only ignore_v4 to True, we reproduce the behavior of the bubble approximation. Notably, while the four-phonon scattering is exceptionally computationally and memory demanding in free energy hessian calculations, within the Lanczos algorithm, accounting for the four-phonon scattering is only a factor two more expensive than using just the third order, without requiring any additional memory.
# Setup the IR response
polarization = np.array([1,0,0]) # Polarization of light
lanczos.prepare_ir(pol_vec = polarization)
Here we tell the Lanczos which kind of calculation we want to do. In other words, we set the \(\boldsymbol{r}\) and \(\boldsymbol{q}\) vectors in Eq.1 for the Lanczos calculation. - prepare_ir - prepare_raman - prepare_mode - prepare_perturbation
The names are intuitive; besides the Raman and IR, prepare_mode allows you to study the response function of a specific phonon mode, and prepare_perturbation enables defining a custom perturbation function.
# Run the algorithm
n_iterations = 1000
lanczos.run_FT(n_iterations)
lanczos.save_status("ir_xpol")
Here we start the calculation of the response function. The number of iterations indicates how many Lanczos steps are required. Each step adds a new pole to the green function. Therefore, many steps are necessary to converge broad spectrum features, while much less if the peaks are sharp. We save the status in such a way that we can get it back later.
Last, the commented line
lanczos.mode = DL.MODE_FAST_JULIA
This line only works if Julia and PyCall are correctly set up in the PC; in that case, run the script with python-jl instead of python. It will exploit a massive speedup of a factor between 10x and 15x. The calculation can also be run in parallel using mpirun before calling the Python executable (or python-jl). In this case, to work correctly, you should have mpi4py installed and working.
Exercise
Compute the Lanczos with the bubble approximation and without any approximation, and check the differences.
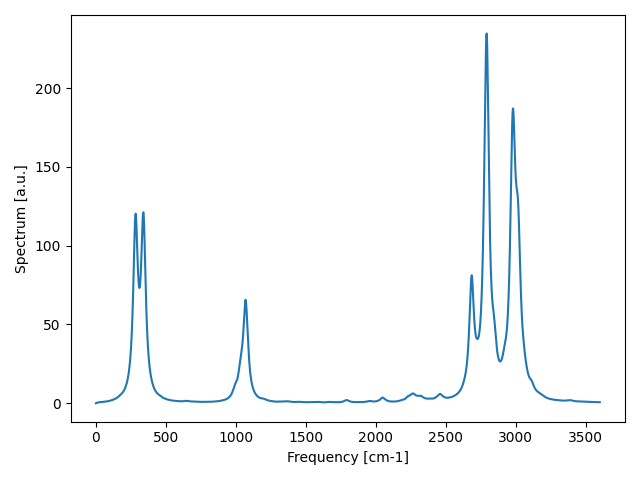
Fig. 13 IR signal accounting for the three-phonon scattering
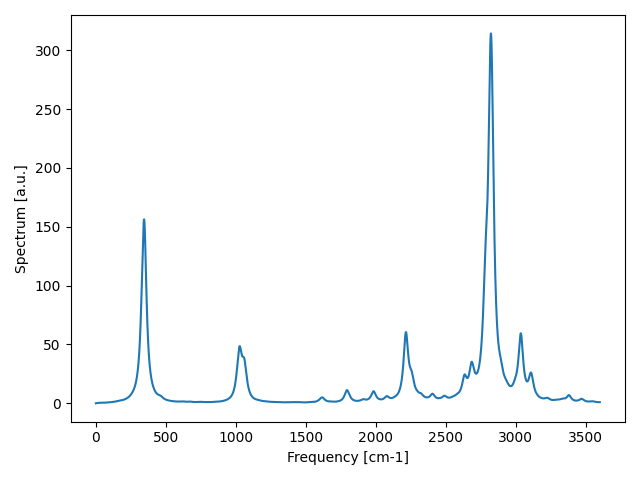
Fig. 14 IR signal accounting for all anharmonic scattering. The peaks that appear slightly below 2500 cm-1 is a combination mode known to be present in ice. See Cherubini et al, J Chem Phys 155, 184502, 2021
Exercise
Try to see how different polarization of the light affects the result.
Analyze the output
In the last part, we employed the script tdscha-plot.py to display the simulation result. This is a quick way to show the results of a calculation.
Here, we will dive deeper into the calculation output file to extract the response function and get the results.
The Lanczos algorithm provides a set of coefficients \(a_i\), \(b_i\), and \(c_i\) through which the green function is evaluated thanks to a continued fraction:
Each iteration of the algorithm adds a new set of coefficients written in the standard output. Thanks to this expression, we only need the series of coefficients to compute the dynamical Green function at any frequency and with any smearing. The Green function can be computed with:
green_function = lanczos.get_green_function_continued_fraction(frequencies, smearing=smearing)
Here frequencies is an array in Rydberg.
The response function is the opposite of the imaginary part of the green function; thus, to reproduce the plot, we have:
import tdscha, tdscha.DynamicalLanczos
import cellconstructor as CC, cellconstructor.Units
import numpy as np
import matplotlib.pyplot as plt
# Load the result of the previous calculation
lanczos = tdscha.DynamicalLanczos.Lanczos()
lanczos.load_status("ir_xpol_v4")
# Get the green function
W_START = 0
W_END = 3700
N_W = 10000
SMEARING = 10
frequencies = np.linspace(W_START, W_END, N_W)
# Convert in RY
frequencies_ry = frequencies / CC.Units.RY_TO_CM
smearing_ry = SMEARING / CC.Units.RY_TO_CM
# Compute the green function
green_function = lanczos.get_green_function_continued_fraction(frequencies_ry,
smearing=smearing_ry)
# Get the response function
ir_response_function = - np.imag(green_function)
# Plot the data
plt.plot(frequencies, ir_response_function)
plt.show()
The previous script plots the data, precisely like plot-tdscha.py; however, now you have full access to the response function, both its imaginary and real parts.
Exercise
Plot the IR data at various smearing and as a function of the number of steps (50, 100, 200, 300, and 1000). How does the signal change with smearing and the number of steps? When is it converged?
Raman response
The Raman response is very similar to the IR. Raman probes the fluctuations of the polarizability instead of those of the polarization, and it occurs when the samples interact with two light sources: the incoming electromagnetic radiation and the outcoming one. The outcoming radiation has a frequency that is shifted with respect to the incoming one by the energy of the scattering phonons. The signal on the red side of the pump is called Stokes, while the signal on the blue side is the Antistokes. Since the outcoming radiation has higher energy than the incoming one in the Antistokes, it is generated only by existing (thermally excited phonons) inside the sample. Therefore it has a lower intensity than the Stokes.
On the Stokes side, the intensity of the scattered light with a frequency redshift of \(\omega\) is
where \(\alpha\) is the polarizability along the \(xy\) axis. We can do a linear expansion around the equilibrium position of the polarizability, and we get:
If we insert it in the expression of the intensity, the average between the positions is the atomic green function divided by the square root of the masses, and we get
where \(G_{ab}(\omega)\) is the atomic green function on atoms \(a\) and \(b\), while \(\Xi_{xy a}\) is the Raman tensor along the electric fields directed in \(x\) and \(y\) and on atom \(a\).
The multiplication factor \(n(\omega) + 1\) comes from the observation of the Stokes nonresonant Raman (it would be just \(n(\omega)\) for the antistokes).
As we did for the IR signal, we can prepare the calculation of the Raman raman scattering by computing the polarizability-polarizability.
# Setup the polarized Raman response
polarization_in = np.array([1,0,0])
polarization_out = np.array([1,0,0])
lanczos.prepare_raman(pol_vec_in=polarization_in,
pol_vec_out=polarization_out)
Note that here we have to specify two polarization of the light, the incoming radiation, and the outcoming radiation.
Exercise
Compute and plot the Intensity of the Raman in the Stokes and antistokes configurations. Try with different polarization and even orthogonal polarization; what does it change?
The Bose-Einstein factor \(n(\omega)\) can be computed with the following function:
# n(w) Bose-Einstein occupation number:
# w is in Ry, T is in K
n_w = tdscha.DynamicalLanczos.bose_occupation(w, T)
Unpolarize Raman and IR
In the previous section, we saw how to compute Raman and IR with specific polarization of the incoming and outcoming radiation, and on oriented crystals (single crystals). However, the most common situation is a powder sample probed with unpolarized light.
In this case, we need to look at the Raman and IR response for unpolarized samples. While this is just the average of the IR signal’s x, y, and z, the Raman is more complex. In particular, unpolarized Raman signal can be computed from the so-called invariants, where the perturbations in the polarizations are the following:
The total Intensity of unpolarized Raman is:
The tdscha code implements a way to compute each perturbation separately. For example, the Raman response related to \(I_A\) is calculated with
lanczos.prepare_raman(unpolarized=0)
While the \(I_{B_i}\) is computed using index \(i\). For example, to compute \(I_{B_5}\):
# To compute I_B5 we do
lanczos.prepare_raman(unpolarized=5)
To get the total spectrum, you need to add the scattering factor \(n(\omega) + 1\) and sum all these perturbation with the correct prefactor (45 for \(I_A\) and 7 for the sum of all \(I_B\)).
To reset a calculation and start a new one, you can use
lanczos.reset()
which may be called before preparing the perturbation.
Exercise
Compute the unpolarized Raman spectrum of ice and plot the results.
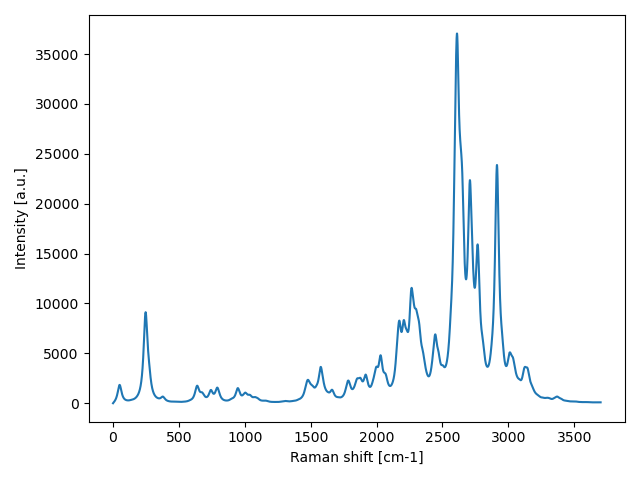
You should employ a supercell size sufficiently big to converge the simulation properly. In this case, the 1x1x1 supercell is too tiny to converge the calculation and get meaningful results.